Angulos

Ángulos

• Angulo Adyacentes
• Ángulo Suplementario
• Ángulo Complementario
• Angulo Obtuso
• Angulo Recto
• Angulo Agudo

Angulo Adyacentes

Un ángulo es considerado adyacente cuando tienen un ángulo y un vértice en común, a la vez que sus demás lados son semirrectas contrarias, a su vez los ángulos adyacentes pueden ser consecutivos y suplementarios, puesto que al unirse se asemejan a un ángulo llano, sin tener un punto interior en común.

 

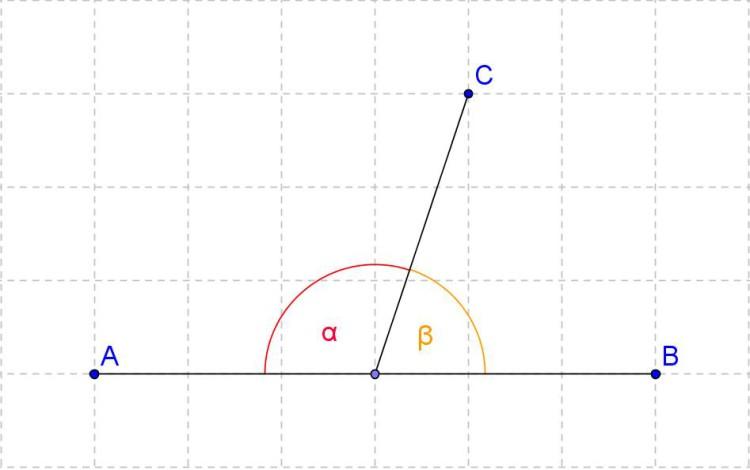
Se consideran suplementarios porque al sumarlos da igual a 180º. La propiedad de los ángulos es que son suplementarios. Entre las propiedades que comprenden los ángulos adyacentes tenemos:

Los senos de los ángulos son iguales.

Los cosenos de los ángulos son iguales pero de signo inverso.

A su vez los ángulos adyacentes internos se podrían desglosar de la siguiente manera:

Los ángulos complementarios, son dos ángulos que al sumarlos su mediciones de 90º

Los ángulos suplementarios, son dos ángulos que al sumarlos su medición es de 180º.

Los ángulos conjugados son dos ángulos que al sumarlos su medición es de 360º.

En ingles se le da el nombre de “adjacent angles” a las parejas de ángulos consecutivos, aun si no son suplementarios. Es muy importante que al revisar los diferentes textos de geometría o matemáticas en donde se mencione el tema de los ángulos, se debe tener presente en cuales términos está siendo utilizado o abordado dicho contenido, ya que en unos textos a los ángulos adyacentes se les llama ángulos consecutivos. Los ángulos adyacentes tienen determinados un lado y un vértice en común originando que sus otros lados se deriven en dos semirrectas opuestas, algunos incorporan entre los ángulos adyacentes a los que comparten un lado y el vértice, aunque no sean suplementarios.

Angulo Suplementario

Los ángulos suplementarios son aquellos que en par suman 180 grados. A diferencia de los ángulos complementarios que forman 90 grados. Siguiendo la misma propiedad y fórmula de los que se complementan entre sí, un ángulo que tenga menos de 180 grados le corresponderá un ángulo que lo suplementa según la fórmula A (ángulo suplementario) = 180° menos (-) el ángulo que necesita suplemento. Ejemplo: A = 180° – 150° = 30°. 

El suplementario de un ángulo de 45° es otro de 135°. El suplementario de un ángulo de 179° es otro de 1°. El suplementario de un ángulo de 90° es otro de la misma medida.

Su aplicación en la práctica es técnica, activa para el cálculo de ángulos arquitectónicos y de importancia en la construcción, al segmentar una circunferencia crear una línea de diámetro y este picarlo en cualquier punto obteniendo dos cuartos de circunferencia, estamos obteniendo un ángulo con su suplementario.

En la vida cotidiana las manillas de un reloj constantemente crear diversos ángulos complementarios. Los ángulos suplementarios son comunes en aquellas estructuras que soportan grandes pesos, como la carpa de un circo, la cual está fijada al piso (superficie plana) la cuerda atada a la estaca forma un ángulo, que suplementa el espacio restante hasta el suelo. En puentes de arco también se pueden apreciar ángulos suplementarios en las bases, al igual, forman un ángulo que se suplementa con el otro formado en el vacío. Una viga perpendicular al suelo puede formar dos ángulos complementarios entre sí (de 90°).

Ángulo complementarios

Los ángulos complementarios son los que sumados son iguales al valor de un ángulo recto, es decir, un ángulo de 90 grados. En caso de que los lados que son comunes estén uno al lado del otro (consecutivos) el ángulo recto se apreciara, sin embargo no necesariamente los ángulos complementarios tienen que ser consecutivos, basta que la suma de ambos sea de 90º. Por ejemplo los dos ángulos no rectos de un triángulo rectángulo, son complementarios y no son consecutivos.

Para calcular la dimensión de un ángulo complementario se toma como referencia un ángulo recto y se le resta el primer ángulo al que se le busca el complemento. Entonces queda un ejemplo así: El ángulo recto es igual a 90° menos el ángulo que tenemos que es de 60°, el ángulo complementario es de 30°.

Siendo o no consecutivos, los ángulos complementarios siempre sumarán matemáticamente 90 grados. Habiendo entendido bien el ejemplo, el ángulo de 30 grados es el complemento del primero, dichos ángulos forman un triángulo rectángulo puesto que los ángulos en un triángulo rectángulo son uno de 90º y los otros dos deben sumar 90 con el del cateto adyacente y se multiplica por la hipotenusa. Por tanto, el seno de α es igual al coseno de β y el seno de β igual al coseno de α puesto que pertenecen al mismo triángulo rectángulo.

La diagonal de un rectángulo también configura ángulos complementarios (90°) con los lados adyacentes. La luz forma a través de un lente ángulos complementarios no consecutivos.

Angulo Obtuso

La diagonal de un rectángulo también configura ángulos complementarios (90°) con los lados adyacentes. La luz forma a través de un lente ángulos complementarios no consecutivos.

El ángulo obtuso es el espacio entre dos rectas que comparten un mismo vértice cuya inclinación o abertura es mayor que 90 grados (90°) y menor que 180 grados (180°).

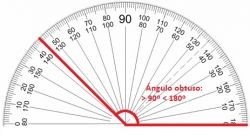
El ángulos obtusos se pueden encontrar, por ejemplo, en los triángulos obtusángulos ya que se caracterizan precisamente por tener uno de sus ángulos obtuso, o sea, mayor a 90 grados y menor a 180 grados.

En geometría, es importante saber identificar los ángulos obtusos, ya que, al ser visualmente mayor de 90° (un cuarto de un círculo), se hace visualmente más fácil determinar, por ejemplo, que sus ángulos suplementarios (ángulos que sumados dan 180 grados) deben ser agudos (menores de 90 grados) y otras operaciones básicas en trigonometría.

Angulo recto

El origen de la palabra proviene del latín Obtusus haciendo alusión a no tener punta o despuntado, embotar, esta palabra se usa en sentido figurativo ya que en su traducción exacta es algo como sin punta, del latín “Obtundere” de allí el uso más apropiado en las matemáticas o geometría, haciendo referencias a los objetos que no tienen puntas o no disponen de ellas; ya sea porque son así o por desgaste la perdieron desmejorando la calidad del objeto o perdiendo así su utilidad para dichos casos son requeridos.

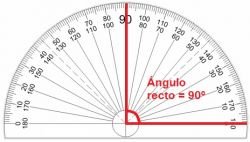
El ángulo recto es el espacio entre dos rectas que comparten el mismo vértice y cuya apertura es de 90 grados (90º).

ángulo recto En geometría, el ángulo recto es importante, ya que, es fácil determinar cuando se encuentran dos rectas perpendiculares, por ejemplo:

En la geometría analítica se obtienen planos cartesianos,

En trigonometría, se puede determinar de manera más rápida e intuitiva los ángulos que componen un triángulo. En un triángulo rectángulo, podemos distinguir fácilmente el ángulo recto y, por ende, concluir que los otros dos ángulos son agudos o menores de 90º.

Además, los ángulos rectos o ángulos de 90 grados es la referencia entre los de menor (ángulos agudos) y de mayor grado (ángulos obtusos) lo que, una vez más, ayuda a visualizar y determinar los tipos de ángulos de las figuras geométricas estudiadas.

Angulo agudo

angulo agudo En geometría, es importante saber identificar los ángulos agudos ya que al ser visualmente menos de 90° (un cuarto de un círculo), se hace más fácil una identificación visual aproximada del tipo de ángulos dentro de un triángulo o dentro de un plano.

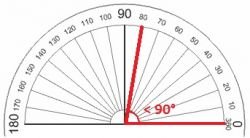
Los ángulos agudos se pueden encontrar, por ejemplo, en los triángulos equiláteros ya que se caracterizan precisamente de ser compuesto por tres ángulos agudos, o sea, tres ángulos de menos de 60°.

En la trigonometría, ciencia que estudia la relación de los elementos de un triángulo rectángulo, los ángulos agudos pueden ser identificados teniendo en cuenta:

La suma de los ángulos interiores de un triángulo suman 180°,

el triángulo rectángulo se compone de un ángulo de 90° por lo tanto los otros dos ángulos deben sumar 90° (ángulos complementarios),

Si dos ángulos suman 90°, entonces ambos son ángulos agudos.

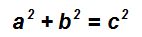
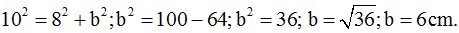
Clasificación de triángulos según su angulo

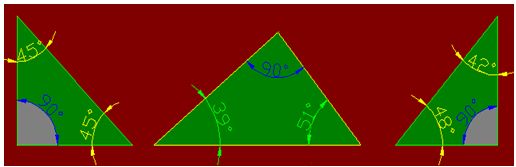
1) Triángulos rectángulos si tienen UN ángulo recto.

Tienes a continuación tres ejemplos de triángulos rectángulos

En un triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa y los lados perpendiculares que forman el ángulo recto se llaman catetos.

Teorema de Pitágoras: Al estudiar el triángulo rectángulo hemos de conocer perfectamente este teorema que nos dice:

En todo triángulo rectángulo, la suma de los cuadrado de los catetos es igual al cuadrado de la hipotenusa

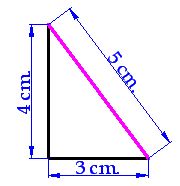
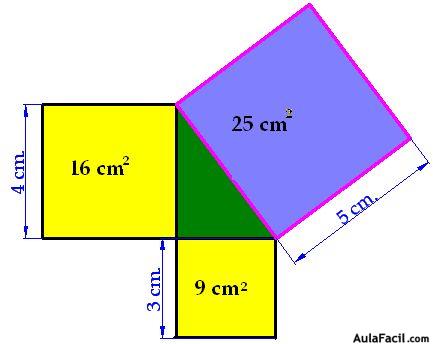
Tomemos como ejemplo el de la figura en el que los catetos miden 3 y 4 cm., respectivamente y 5 cm., la hipotenusa.

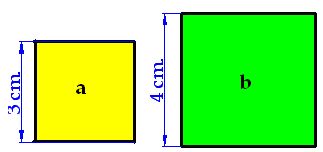
Con las medidas de los catetos  formamos cuadrados 

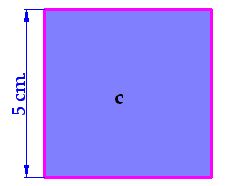
Con la longitud de la hipotenusa formamos otro cuadrado (c):

Si calculas el área del cuadrado formado por el cateto (a): lado al cuadrado obtienes como valor del área: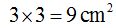 

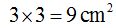
Si a continuación calculas el cuadrado formado por el cateto (b), el valor de su área vale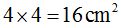 

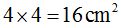
El cuadrado formado por la longitud de la hipotenusa tiene un área  de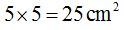 

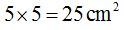
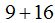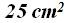
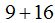Si sumas las áreas de los cuadrados de los catetos, es decir  obtienes el área formada por el cuadrado de la hipotenusa,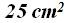 

Fíjate en la figura siguiente:

La suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.Siendo a y b las longitudes de los catetos los catetos, y c la longitud de la hipotenusa podemos escribir:

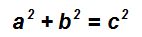
Resuelve:

(a) Calcula la longitud de la hipotenusa de un triángulo rectángulo sabiendo que los catetos miden 5 y 6 cm., respectivamente.

El resultado es de 7,81 cm. porque la suma de los cuadrados de los catetos es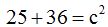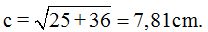 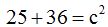 de donde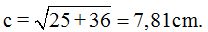 

(b) Sabiendo que la hipotenusa de un triángulo rectángulo vale 10 cm., y uno de los catetos 8 cm.

¿Cuál es el valor del otro cateto?

El resultado es de 6 cm. Porque 

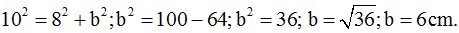
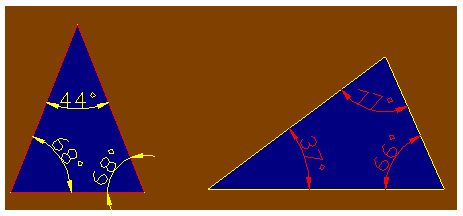
2) Triángulos acutángulos, si tienen TRES ángulos agudos(menores de 90º).

En el dibujo siguiente tienes dos triángulos acutángulos.

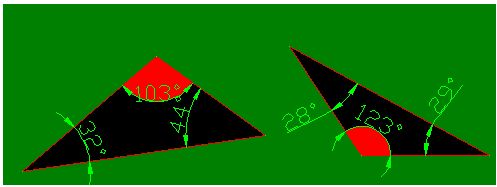
3) Triángulos obtusángulos, si tienen UN ángulo obtuso (más de 90º).

En la siguiente figura tienes dos triángulos obtusángulos

15.76  ¿Puede un triángulo rectángulo tener, además de su ángulo recto, dos ángulos de 56º y 45º? ¿Por qué?

Respuesta: No, porque la suma de los tres ángulos debe valer 180º y en este caso, supera ese número.

15.77  Dos triángulos isósceles tienen iguales dos lados y el ángulo comprendido entre ellos. ¿Son necesariamente iguales?

Respuesta: Sí.

15.78  ¿La suma de los ángulos no rectos de los triángulos rectángulos han de sumar un ángulo recto? ¿Por qué?

Respuesta: Sí, porque si el ángulo recto vale 90º los otros dos 2 ángulos no rectos tendrán que sumar 90º, de este modo, la suma de los ángulos del triángulo suman 180º

RELACIÓN ENTRE LOS ÁNGULOS Y LOS LADOS DE LOS TRIÁNGULOS

En los triángulos los ángulos dependen de los lados en cuanto a sus  medidas, de ahí que podemos decir: 

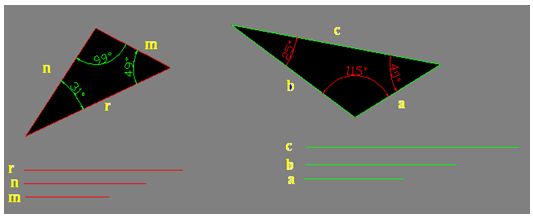
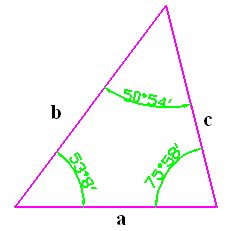
A) A mayor lado se opone mayor ángulo

Comprueba en la figura siguiente que a mayor lado, se oponemayor ángulo.

Lo mismo puede decirse a la inversa, a menor ángulo, se opone menor longitud de lado

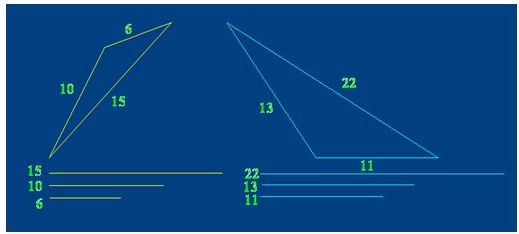
B) En un triángulo, la longitud de  un lado cualquiera es menor que la suma de las longitudes de los otros dos lados.

La suma de los dos lados menores será siempre mayor que el lado más grande.

En el primer triángulo la suma de los lados de menor longitud es mayor que la del lado de mayor longitud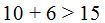 

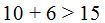
Lo mismo sucede en el segundo triángulo de la figura: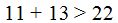 

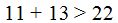
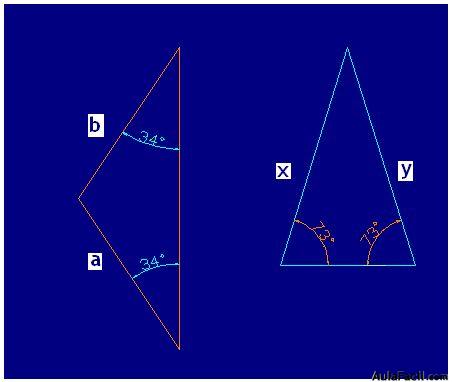
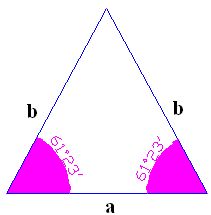
C) Si un triángulo tiene sus lados iguales también serán sus ángulos opuestos.

En la figura siguiente verás en el primer triángulo que los lados a y b al tener iguales longitudes, sus ángulos opuestos miden lo mismo.

Igualmente, en el segundo triángulo los lados x  e  y  al tener la misma longitud, sus ángulos opuestos son iguales.

triángulos equiláteros

Las palabras equi - látero vienen del latín: igual – lado.

Son los triángulos cuyos tres lados son iguales: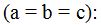 

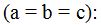
 triángulos isósceles

La palabra isósceles está compuesta de dos palabras griegas isoque significa igual y de la palabra skeles que podemos traducir por piernas.

La palabra isósceles referido a la geometría quiere decir que dos lados (piernas) son iguales. Por lo tanto, un triángulo con dos lados iguales llamamos isósceles.

Como ves en la figura, tienes el triángulo isósceles con dos lados iguales. Si tiene 2 lados iguales tendrá también dos ángulos iguales.

triángulos escalenos

La palabra escaleno procede de la palabra griega skaleno que significa cojear, cojo. Nos da la idea que si el triángulo “cojea” sus lados no son iguales. Efectivamente, el triángulo escaleno tiene sus lados diferentes por lo que sus ángulos también serán diferentes.